Function Types for GCP

>> Tensor Toolbox >> CP Decompositions >> GCP-OPT >> Function Types for GCP

The GCP capability of the Tensor Toolbox allows the user to specify a fit function. There are a number of ''standard'' choices that we provide via the helper function tt_gcp_fg_setup function. These choices are presented in detail below. Motivations and details for these choices can be found in:

These choices can be passed directly to gcp_opt via the 'type' option. To test the options, call the hidden function:

[f,g,lowerbnd] = tt_gcp_fg_setup(type)

We discuss the choices for the type below.

Contents

Gaussian (real-valued data)

This is indicated by specifying the type as either 'normal' or 'gaussian'. This choice correspond to standard CP, which is implemented in cp_als and cp_opt. It is useful for continuous real-valued data tensors. This choice specifies

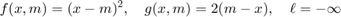
$$f(x,m) = (x-m)^2, \quad g(x,m) = 2(m-x), \quad \ell=-\infty$$

[f,g,lowerbnd] = tt_gcp_fg_setup('normal')

f =
  function_handle with value:
    @(x,m)(m-x).^2
g =
  function_handle with value:
    @(x,m)2.*(m-x)
lowerbnd =
  -Inf

Poisson (count data)

This is indicated by specifying the type as either 'count' or 'poisson'. This choice is useful for count data tensors, i.e., tensors that have only entries in {0,1,2,...}. This choice corresponds to Poisson CP, which is implemente din cp_apr. This choice specifies

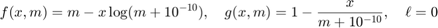
$$f(x,m) = m - x \log(m + 10^{-10}), \quad g(x,m) = 1 - \frac{x}{m+10^{-10}}, \quad \ell=0$$

The quantity 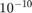$10^{-10}$ is a fudge factor to avoid divide-by-zero errors.

[f,g,lowerbnd] = tt_gcp_fg_setup('count')

f =
  function_handle with value:
    @(x,m)m-x.*log(m+1e-10)
g =
  function_handle with value:
    @(x,m)1-x./(m+1e-10)
lowerbnd =
     0

Poisson with Log Link (count data)

This is indicated by specifying the type as 'poisson-log'. This choice is useful for count data tensors, i.e., tensors that have only entries in {0,1,2,...}. This choice specifies

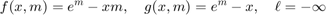
$$f(x,m) = e^m - x m, \quad g(x,m) = e^m - x, \quad \ell=-\infty$$

[f,g,lowerbnd] = tt_gcp_fg_setup('poisson-log')

f =
  function_handle with value:
    @(x,m)exp(m)-x.*m
g =
  function_handle with value:
    @(x,m)exp(m)-x
lowerbnd =
  -Inf

Bernoulli with Odds Link (binary data)

This is indicated by specifying the type as either 'binary' or 'bernoulli-odds'. This choice is useful for binary data tensors, i.e., tensors that have only 0 or 1 entries. This choice specifies

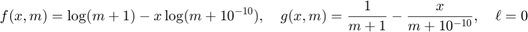
$$f(x,m) = \log(m+1) - x \log(m + 10^{-10}), \quad g(x,m) = \frac{1}{m+1} - \frac{x}{m+10^{-10}}, \quad \ell=0$$

The quantity 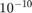$10^{-10}$ is a fudge factor to avoid divide-by-zero errors.

[f,g,lowerbnd] = tt_gcp_fg_setup('binary')

f =
  function_handle with value:
    @(x,m)log(m+1)-x.*log(m+1e-10)
g =
  function_handle with value:
    @(x,m)1./(m+1)-x./(m+1e-10)
lowerbnd =
     0

Bernoulli with Logit Link (binary data)

This is indicated by specifying the type as 'bernoulli-logit'. This choice is useful for binary data tensors, i.e., tensors that have only 0 or 1 entries. This choice specifies

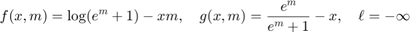
$$f(x,m) = \log(e^m+1) - x m, \quad g(x,m) = \frac{e^m}{e^m+1} - x, \quad \ell=-\infty$$

[f,g,lowerbnd] = tt_gcp_fg_setup('bernoulli-logit')

f =
  function_handle with value:
    @(x,m)log(exp(m)+1)-x.*m
g =
  function_handle with value:
    @(x,m)exp(m)./(exp(m)+1)-x
lowerbnd =
  -Inf

Rayleigh (real-valued data)

This is indicated by specifying the type 'rayleigh'. This choice is useful for nonnegative real-values data tensors, i.e., tensors that have only nonnegative. This choice specifies

$$f(x,m) = 2 \log(m+10^{-10}) - \frac{\pi}{4} \frac{x}{(m + 10^{-10})^2}, \quad g(x,m) = \frac{1}{m+10^{-10}} - \frac{\pi}{2} \frac{x}{(m + 10^{-10})^3}, \quad \ell=0$$

The quantity 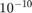$10^{-10}$ is a fudge factor to avoid divide-by-zero errors.

[f,g,lowerbnd] = tt_gcp_fg_setup('rayleigh')

f =
  function_handle with value:
    @(x,m)2*log(m+1e-10)+(pi/4)*(x./(m+1e-10)).^2
g =
  function_handle with value:
    @(x,m)2./(m+1e-10)-(pi/2)*x.^2./(m+1e-10).^3
lowerbnd =
     0

Gamma (nonnegative real-valued data)

This is indicated by specifying the type 'gamma'. This choice is useful for nonnegative real-values data tensors, i.e., tensors that have only nonnegative. This choice specifies

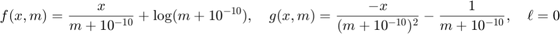
$$f(x,m) = \frac{x}{m+10^{-10}} + \log(m + 10^{-10}), \quad g(x,m) = \frac{-x}{(m+10^{-10})^2} - \frac{1}{m + 10^{-10}}, \quad \ell=0$$

The quantity 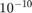$10^{-10}$ is a fudge factor to avoid divide-by-zero errors.

[f,g,lowerbnd] = tt_gcp_fg_setup('gamma')

f =
  function_handle with value:
    @(x,m)x./(m+1e-10)+log(m+1e-10)
g =
  function_handle with value:
    @(x,m)-x./((m+1e-10).^2)+1./(m+1e-10)
lowerbnd =
     0

Huber (nonnegative real-valued data)

This is indicated by specifying the type 'huber (DELTA)', where DELTA is 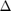$\Delta$ in the equations below. This choice is useful for nonnegative real-values data tensors, i.e., tensors that have only nonnegative. This choice specifies

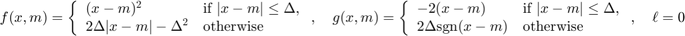
$$f(x,m) = \left\{ \begin{array}{ll}(x-m)^2 & \mbox{if } |x-m| \leq \Delta, \\ 2\Delta|x-m|-\Delta^2 & \mbox{otherwise}\end{array}\right., \quad g(x,m) = \left\{ \begin{array}{ll}-2(x-m) & \mbox{if } |x-m| \leq \Delta, \\ 2\Delta\mbox{sgn}(x-m) & \mbox{otherwise}\end{array}\right., \quad \ell = 0 $$

[f,g,lowerbnd] = tt_gcp_fg_setup('huber (0.25)')

f =
  function_handle with value:
    @(x,m)(x-m).^2.*(abs(x-m)<0.25)+(0.5.*abs(x-m)-0.0625).*(abs(x-m)>=0.25)
g =
  function_handle with value:
    @(x,m)-2.*(x-m).*(abs(x-m)<0.25)-(0.5.*sign(x-m)).*(abs(x-m)>=0.25)
lowerbnd =
  -Inf

Negative Binomial (count data)

This is indicated by specifying the type 'negative-binomial (r)', where r is $r$ in the equations below. This choice is useful for count data tensors. This choice specifies

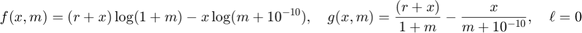
$$f(x,m) = (r+x) \log(1+m) - x \log(m+10^{-10}), \quad g(x,m) = \frac{(r+x)}{1+m} - \frac{x}{m+10^{-10}}, \quad \ell = 0 $$

[f,g,lowerbnd] = tt_gcp_fg_setup('negative-binomial (4)')

f =
  function_handle with value:
    @(x,m)(4+x).*log(1+m)-x*log(m+1e-10)
g =
  function_handle with value:
    @(x,m)(5)./(1+m)-x./(m+1e-10)
lowerbnd =
     0

Beta (nonnegative real-valued data)

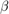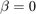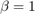This is indicated by specifying the type 'beta (BETA)', where BETA is $\beta$ in the equations below. This choice is useful for nonnegative data tensors. Choices of $\beta=0$ or $\beta=1$ are not allowed because these correspond to 'gamma' or 'rayleigh'. This choice specifies

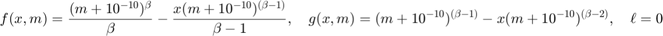
$$f(x,m) = \frac{ (m+10^{-10})^\beta }{\beta} - \frac{x(m+10^{-10})^{(\beta-1)} }{\beta-1}, \quad g(x,m) = (m+10^{-10})^{(\beta-1)} - x(m+10^{-10})^{(\beta-2)}, \quad \ell = 0 $$

[f,g,lowerbnd] = tt_gcp_fg_setup('beta (0.3)')

f =
  function_handle with value:
    @(x,m)(3.33333).*(m+1e-10).^(0.3)-(-1.42857).*x.*(m+1e-10).^(-0.7)
g =
  function_handle with value:
    @(x,m)(m+1e-10).^(-0.7)-x.*(m+1e-10).^(-1.7)
lowerbnd =
     0

Tensor Toolbox for MATLAB: www.tensortoolbox.org.