Kruskal Tensors
Kruskal format is a decomposition of a tensor X as the sum of the outer products as the columns of matrices. For example, we might write
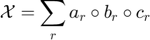
where a subscript denotes column index and a circle denotes outer product. In other words, the tensor X is built from the columns of the matrices A,B, and C. It's often helpful to explicitly specify a weight for each outer product, which we do here:
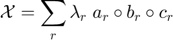
The ktensor class stores the components of the tensor X and can perform many operations, e.g., ttm, without explicitly forming the tensor X.
Contents
- Kruskal tensor format via ktensor
- Specifying weights in a ktensor
- Creating a one-dimensional ktensor
- Constituent parts of a ktensor
- Creating a ktensor from its constituent parts
- Creating an empty ktensor
- Use full or tensor to convert a ktensor to a tensor
- Use double to convert a ktensor to a multidimensional array
- Use tendiag or sptendiag to convert a ktensor to a ttensor.
- Use ndims and size for the dimensions of a ktensor
- Subscripted reference for a ktensor
- Subscripted assignment for a ktensor
- Use end for the last array index.
- Adding and subtracting ktensors
- Basic operations with a ktensor
- Use permute to reorder the modes of a ktensor
- Use arrange to normalize the factors of a ktensor
- Use fixsigns for sign indeterminacies in a ktensor
- Use ktensor to store the 'skinny' SVD of a matrix
- Displaying a ktensor
- Displaying data
Kruskal tensor format via ktensor
Kruskal format stores a tensor as a sum of rank-1 outer products. For example, consider a tensor of the following form.
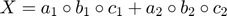
This can be stored in Kruskal form as follows.
rand('state',0); A = rand(4,2); %<-- First column is a_1, second is a_2. B = rand(3,2); %<-- Likewise for B. C = rand(2,2); %<-- Likewise for C. X = ktensor({A,B,C}) %<-- Create the ktensor.
X is a ktensor of size 4 x 3 x 2
X.lambda =
1 1
X.U{1} =
0.9501 0.8913
0.2311 0.7621
0.6068 0.4565
0.4860 0.0185
X.U{2} =
0.8214 0.7919
0.4447 0.9218
0.6154 0.7382
X.U{3} =
0.1763 0.9355
0.4057 0.9169
For Kruskal format, there can be any number of matrices, but every matrix must have the same number of columns. The number of rows can vary.
Y = ktensor({rand(4,1),rand(2,1),rand(3,1)}) %<-- Another ktensor.
Y is a ktensor of size 4 x 2 x 3
Y.lambda =
1
Y.U{1} =
0.4103
0.8936
0.0579
0.3529
Y.U{2} =
0.8132
0.0099
Y.U{3} =
0.1389
0.2028
0.1987
Specifying weights in a ktensor
Weights for each rank-1 tensor can be specified by passing in a column vector. For example,
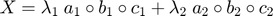
lambda = [5.0; 0.25]; %<-- Weights for each factor. X = ktensor(lambda,{A,B,C}) %<-- Create the ktensor.
X is a ktensor of size 4 x 3 x 2
X.lambda =
5.0000 0.2500
X.U{1} =
0.9501 0.8913
0.2311 0.7621
0.6068 0.4565
0.4860 0.0185
X.U{2} =
0.8214 0.7919
0.4447 0.9218
0.6154 0.7382
X.U{3} =
0.1763 0.9355
0.4057 0.9169
Creating a one-dimensional ktensor
Y = ktensor({rand(4,5)}) %<-- A one-dimensional ktensor.
Y is a ktensor of size 4
Y.lambda =
1 1 1 1 1
Y.U{1} =
0.6038 0.7468 0.4186 0.6721 0.3795
0.2722 0.4451 0.8462 0.8381 0.8318
0.1988 0.9318 0.5252 0.0196 0.5028
0.0153 0.4660 0.2026 0.6813 0.7095
Constituent parts of a ktensor
X.lambda %<-- Weights or multipliers.
ans =
5.0000
0.2500
X.U %<-- Cell array of matrices.
ans =
3×1 cell array
{4×2 double}
{3×2 double}
{2×2 double}
Creating a ktensor from its constituent parts
Y = ktensor(X.lambda,X.U) %<-- Recreate X.
Y is a ktensor of size 4 x 3 x 2
Y.lambda =
5.0000 0.2500
Y.U{1} =
0.9501 0.8913
0.2311 0.7621
0.6068 0.4565
0.4860 0.0185
Y.U{2} =
0.8214 0.7919
0.4447 0.9218
0.6154 0.7382
Y.U{3} =
0.1763 0.9355
0.4057 0.9169
Creating an empty ktensor
Z = ktensor %<-- Empty ktensor.
Z is a ktensor of size [empty tensor] Z.lambda =
Use full or tensor to convert a ktensor to a tensor
full(X) %<-- Converts to a tensor.
ans is a tensor of size 4 x 3 x 2 ans(:,:,1) = 0.8529 0.5645 0.6692 0.3085 0.2549 0.2569 0.5239 0.3362 0.4080 0.3552 0.1945 0.2668 ans(:,:,2) = 1.7450 1.0454 1.3370 0.5235 0.3695 0.4175 1.0940 0.6439 0.8348 0.8131 0.4423 0.6098
tensor(X) %<-- Same as above.
ans is a tensor of size 4 x 3 x 2 ans(:,:,1) = 0.8529 0.5645 0.6692 0.3085 0.2549 0.2569 0.5239 0.3362 0.4080 0.3552 0.1945 0.2668 ans(:,:,2) = 1.7450 1.0454 1.3370 0.5235 0.3695 0.4175 1.0940 0.6439 0.8348 0.8131 0.4423 0.6098
Use double to convert a ktensor to a multidimensional array
double(X) %<-- Converts to an array.
ans(:,:,1) =
0.8529 0.5645 0.6692
0.3085 0.2549 0.2569
0.5239 0.3362 0.4080
0.3552 0.1945 0.2668
ans(:,:,2) =
1.7450 1.0454 1.3370
0.5235 0.3695 0.4175
1.0940 0.6439 0.8348
0.8131 0.4423 0.6098
Use tendiag or sptendiag to convert a ktensor to a ttensor.
A ktensor can be regarded as a ttensor with a diagonal core.
R = length(X.lambda); %<-- Number of factors in X. core = tendiag(X.lambda, repmat(R,1,ndims(X))); %<-- Create a diagonal core. Y = ttensor(core, X.u) %<-- Assemble the ttensor.
Y is a ttensor of size 4 x 3 x 2
Y.core is a tensor of size 2 x 2 x 2
Y.core(:,:,1) =
5 0
0 0
Y.core(:,:,2) =
0 0
0 0.2500
Y.U{1} =
0.9501 0.8913
0.2311 0.7621
0.6068 0.4565
0.4860 0.0185
Y.U{2} =
0.8214 0.7919
0.4447 0.9218
0.6154 0.7382
Y.U{3} =
0.1763 0.9355
0.4057 0.9169
norm(full(X)-full(Y)) %<-- They are the same.
ans = 3.7238e-16
core = sptendiag(X.lambda, repmat(R,1,ndims(X))); %<-- Sparse diagonal core. Y = ttensor(core, X.u) %<-- Assemble the ttensor
Y is a ttensor of size 4 x 3 x 2
Y.core is a sparse tensor of size 2 x 2 x 2 with 2 nonzeros
(1,1,1) 5.0000
(2,2,2) 0.2500
Y.U{1} =
0.9501 0.8913
0.2311 0.7621
0.6068 0.4565
0.4860 0.0185
Y.U{2} =
0.8214 0.7919
0.4447 0.9218
0.6154 0.7382
Y.U{3} =
0.1763 0.9355
0.4057 0.9169
norm(full(X)-full(Y)) %<-- They are the same.
ans = 3.7238e-16
Use ndims and size for the dimensions of a ktensor
ndims(X) %<-- Number of dimensions.
ans =
3
size(X) %<-- Row vector of the sizes.
ans =
4 3 2
size(X,2) %<-- Size of the 2nd mode.
ans =
3
Subscripted reference for a ktensor
X(1,1,1) %<-- Assemble the (1,1,1) element (requires computation).
ans =
0.8529
X.lambda(2) %<-- Weight of 2nd factor.
ans =
0.2500
X.U{2} %<-- Extract a matrix.
ans =
0.8214 0.7919
0.4447 0.9218
0.6154 0.7382
X{2} %<-- Same as above.
ans =
0.8214 0.7919
0.4447 0.9218
0.6154 0.7382
Subscripted assignment for a ktensor
X.lambda = ones(size(X.lambda)) %<-- Insert new multipliers.
X is a ktensor of size 4 x 3 x 2
X.lambda =
1 1
X.U{1} =
0.9501 0.8913
0.2311 0.7621
0.6068 0.4565
0.4860 0.0185
X.U{2} =
0.8214 0.7919
0.4447 0.9218
0.6154 0.7382
X.U{3} =
0.1763 0.9355
0.4057 0.9169
X.lambda(1) = 7 %<-- Change a single element of lambda.
X is a ktensor of size 4 x 3 x 2
X.lambda =
7 1
X.U{1} =
0.9501 0.8913
0.2311 0.7621
0.6068 0.4565
0.4860 0.0185
X.U{2} =
0.8214 0.7919
0.4447 0.9218
0.6154 0.7382
X.U{3} =
0.1763 0.9355
0.4057 0.9169
X{3}(1:2,1) = [1;1] %<-- Change the matrix for mode 3.
X is a ktensor of size 4 x 3 x 2
X.lambda =
7 1
X.U{1} =
0.9501 0.8913
0.2311 0.7621
0.6068 0.4565
0.4860 0.0185
X.U{2} =
0.8214 0.7919
0.4447 0.9218
0.6154 0.7382
X.U{3} =
1.0000 0.9355
1.0000 0.9169
Use end for the last array index.
X(3:end,1,1) %<-- Calculated X(3,1,1) and X((4,1,1).
ans =
3.8274
2.8080
X(1,1,1:end-1) %<-- Calculates X(1,1,1).
ans =
6.1234
X{end} %<-- Or use inside of curly braces. This is X{3}.
ans =
1.0000 0.9355
1.0000 0.9169
Adding and subtracting ktensors
Adding two ktensors is the same as concatenating the matrices
X = ktensor({rand(4,2),rand(2,2),rand(3,2)}) %<-- Data.
Y = ktensor({rand(4,2),rand(2,2),rand(3,2)}) %<-- More data.
X is a ktensor of size 4 x 2 x 3
X.lambda =
1 1
X.U{1} =
0.4289 0.6822
0.3046 0.3028
0.1897 0.5417
0.1934 0.1509
X.U{2} =
0.6979 0.8600
0.3784 0.8537
X.U{3} =
0.5936 0.8216
0.4966 0.6449
0.8998 0.8180
Y is a ktensor of size 4 x 2 x 3
Y.lambda =
1 1
Y.U{1} =
0.6602 0.5341
0.3420 0.7271
0.2897 0.3093
0.3412 0.8385
Y.U{2} =
0.5681 0.7027
0.3704 0.5466
Y.U{3} =
0.4449 0.7948
0.6946 0.9568
0.6213 0.5226
Z = X + Y %<-- Concatenates the factor matrices.
Z is a ktensor of size 4 x 2 x 3
Z.lambda =
1 1 1 1
Z.U{1} =
0.4289 0.6822 0.6602 0.5341
0.3046 0.3028 0.3420 0.7271
0.1897 0.5417 0.2897 0.3093
0.1934 0.1509 0.3412 0.8385
Z.U{2} =
0.6979 0.8600 0.5681 0.7027
0.3784 0.8537 0.3704 0.5466
Z.U{3} =
0.5936 0.8216 0.4449 0.7948
0.4966 0.6449 0.6946 0.9568
0.8998 0.8180 0.6213 0.5226
Z = X - Y %<-- Concatenates as with plus, but changes the weights.
Z is a ktensor of size 4 x 2 x 3
Z.lambda =
1 1 -1 -1
Z.U{1} =
0.4289 0.6822 0.6602 0.5341
0.3046 0.3028 0.3420 0.7271
0.1897 0.5417 0.2897 0.3093
0.1934 0.1509 0.3412 0.8385
Z.U{2} =
0.6979 0.8600 0.5681 0.7027
0.3784 0.8537 0.3704 0.5466
Z.U{3} =
0.5936 0.8216 0.4449 0.7948
0.4966 0.6449 0.6946 0.9568
0.8998 0.8180 0.6213 0.5226
norm( full(Z) - (full(X)-full(Y)) ) %<-- Should be zero.
ans = 1.8968e-16
Basic operations with a ktensor
+X %<-- Calls uplus.
ans is a ktensor of size 4 x 2 x 3
ans.lambda =
1 1
ans.U{1} =
0.4289 0.6822
0.3046 0.3028
0.1897 0.5417
0.1934 0.1509
ans.U{2} =
0.6979 0.8600
0.3784 0.8537
ans.U{3} =
0.5936 0.8216
0.4966 0.6449
0.8998 0.8180
-X %<-- Calls uminus.
ans is a ktensor of size 4 x 2 x 3
ans.lambda =
-1 -1
ans.U{1} =
0.4289 0.6822
0.3046 0.3028
0.1897 0.5417
0.1934 0.1509
ans.U{2} =
0.6979 0.8600
0.3784 0.8537
ans.U{3} =
0.5936 0.8216
0.4966 0.6449
0.8998 0.8180
5*X %<-- Calls mtimes.
ans is a ktensor of size 4 x 2 x 3
ans.lambda =
5 5
ans.U{1} =
0.4289 0.6822
0.3046 0.3028
0.1897 0.5417
0.1934 0.1509
ans.U{2} =
0.6979 0.8600
0.3784 0.8537
ans.U{3} =
0.5936 0.8216
0.4966 0.6449
0.8998 0.8180
Use permute to reorder the modes of a ktensor
permute(X,[2 3 1]) %<-- Reorders modes of X
ans is a ktensor of size 2 x 3 x 4
ans.lambda =
1 1
ans.U{1} =
0.6979 0.8600
0.3784 0.8537
ans.U{2} =
0.5936 0.8216
0.4966 0.6449
0.8998 0.8180
ans.U{3} =
0.4289 0.6822
0.3046 0.3028
0.1897 0.5417
0.1934 0.1509
Use arrange to normalize the factors of a ktensor
The function arrange normalizes the columns of the factors and then arranges the rank-one pieces in decreasing order of size.
X = ktensor({rand(3,2),rand(4,2),rand(2,2)}) % <-- Unit weights.
X is a ktensor of size 3 x 4 x 2
X.lambda =
1 1
X.U{1} =
0.8801 0.2714
0.1730 0.2523
0.9797 0.8757
X.U{2} =
0.7373 0.1991
0.1365 0.2987
0.0118 0.6614
0.8939 0.2844
X.U{3} =
0.4692 0.9883
0.0648 0.5828
arrange(X) %<-- Normalized and rearranged.
ans is a ktensor of size 3 x 4 x 2
ans.lambda =
0.8778 0.7342
ans.U{1} =
0.2855 0.6626
0.2653 0.1302
0.9209 0.7376
ans.U{2} =
0.2475 0.6319
0.3713 0.1170
0.8221 0.0101
0.3535 0.7661
ans.U{3} =
0.8614 0.9906
0.5079 0.1368
Use fixsigns for sign indeterminacies in a ktensor
The largest magnitude entry for each factor is changed to be positive provided that we can flip the signs of pairs of vectors in that rank-1 component.
Y = X;
Y.u{1}(:,1) = -Y.u{1}(:,1); % switch the sign on a pair of columns
Y.u{2}(:,1) = -Y.u{2}(:,1)
Y is a ktensor of size 3 x 4 x 2
Y.lambda =
1 1
Y.U{1} =
-0.8801 0.2714
-0.1730 0.2523
-0.9797 0.8757
Y.U{2} =
-0.7373 0.1991
-0.1365 0.2987
-0.0118 0.6614
-0.8939 0.2844
Y.U{3} =
0.4692 0.9883
0.0648 0.5828
fixsigns(Y)
ans is a ktensor of size 3 x 4 x 2
ans.lambda =
1 1
ans.U{1} =
0.8801 0.2714
0.1730 0.2523
0.9797 0.8757
ans.U{2} =
0.7373 0.1991
0.1365 0.2987
0.0118 0.6614
0.8939 0.2844
ans.U{3} =
0.4692 0.9883
0.0648 0.5828
Use ktensor to store the 'skinny' SVD of a matrix
A = rand(4,3) %<-- A random matrix.
A =
0.4235 0.2259 0.6405
0.5155 0.5798 0.2091
0.3340 0.7604 0.3798
0.4329 0.5298 0.7833
[U,S,V] = svd(A,0); %<-- Compute the SVD. X = ktensor(diag(S),{U,V}) %<-- Store the SVD as a ktensor.
X is a ktensor of size 4 x 3
X.lambda =
1.7002 0.5095 0.2277
X.U{1} =
-0.4346 -0.5816 0.3635
-0.4365 0.5184 0.6947
-0.5109 0.4983 -0.5366
-0.5996 -0.3804 -0.3120
X.U{2} =
-0.4937 0.0444 0.8685
-0.6220 0.6800 -0.3883
-0.6078 -0.7319 -0.3080
double(X) %<-- Reassemble the original matrix.
ans =
0.4235 0.2259 0.6405
0.5155 0.5798 0.2091
0.3340 0.7604 0.3798
0.4329 0.5298 0.7833
Displaying a ktensor
disp(X) %<-- Displays the vector lambda and each factor matrix.
ans is a ktensor of size 4 x 3
ans.lambda =
1.7002 0.5095 0.2277
ans.U{1} =
-0.4346 -0.5816 0.3635
-0.4365 0.5184 0.6947
-0.5109 0.4983 -0.5366
-0.5996 -0.3804 -0.3120
ans.U{2} =
-0.4937 0.0444 0.8685
-0.6220 0.6800 -0.3883
-0.6078 -0.7319 -0.3080
Displaying data
The datadisp function allows the user to associate meaning to the modes and display those modes with the most meaning (i.e., corresponding to the largest values).
X = ktensor({[0.8 0.1 1e-10]',[1e-5 2 3 1e-4]',[0.5 0.5]'}); %<-- Create tensor.
X = arrange(X) %<-- Normalize the factors.
X is a ktensor of size 3 x 4 x 2
X.lambda =
2.0555
X.U{1} =
0.9923
0.1240
0.0000
X.U{2} =
0.0000
0.5547
0.8321
0.0000
X.U{3} =
0.7071
0.7071
labelsDim1 = {'one','two','three'}; %<-- Labels for mode 1.
labelsDim2 = {'A','B','C','D'}; %<-- Labels for mode 2.
labelsDim3 = {'on','off'}; %<-- Labels for mode 3.
datadisp(X,{labelsDim1,labelsDim2,labelsDim3}) %<-- Display.
======== Group 1 ======== Weight = 2.055480 Score Id Name 0.9922779 1 one 0.1240347 2 two Score Id Name 0.8320503 3 C 0.5547002 2 B 2.774e-05 4 D 2.774e-06 1 A Score Id Name 0.7071068 1 on 0.7071068 2 off
