Sum of Structured Tensors
When certain operations are performed on a tensor which is formed as a sum of tensors, it can be beneficial to avoid explicitly forming the sum. For example, if a tensor is formed as a sum of a low rank tensor and a sparse tensor, the structure of the summands can make storage, decomposition and operations with other tensors significantly more efficient. The tensor toolbox supports a sumtensor object designed to exploit this structure. Here we explain the basics of defining and using sumtensors.
Contents
- Creating sumtensors
- An Large-Scale Example
- Further examples of the sumtensor constructer
- Use ndims and size for the dimensions of a sumtensor
- Use full to convert a sumtensor to a "generic" tensor
- Use double to convert a sumtensor to a multidimensional array
- Matricized Khatri-Rao product of a sumtensor
- Use innerprod to compute the inner product of a sumtensor
- Use norm for compatibility with the other types of tensors.
- Use CP-ALS to find a CP decomposition of a sumtensor
- Basic operations (plus) for sumtensors
- Subscripted reference for sumtensors
Creating sumtensors
A sumtensor T can only be delared as a sum of same-sized tensors T1, T2,...,TN. The summand tensors are stored in a cell array, which define the "parts" of the sumtensor. The parts of a sumtensor can be (generic) tensors (as tensor), sparse tensors (as sptensor), Kruskal tensors (as ktensor), or Tucker tensors (as ttensor). An example of the use of the sumtensor constructor follows.
T1 = tensor(ones(3,3,3)); %<--A tensor T2 = sptensor([1 1 1; 2 2 2; 3 3 2; 2 1 1], 1, [3,3,3]); %<--A sparse tensor T = sumtensor(T1,T2)
T is a sumtensor of size 3 x 3 x 3 with 2 parts
T.part{1} is a tensor of size 3 x 3 x 3
T.part{1}(:,:,1) =
1 1 1
1 1 1
1 1 1
T.part{1}(:,:,2) =
1 1 1
1 1 1
1 1 1
T.part{1}(:,:,3) =
1 1 1
1 1 1
1 1 1
T.part{2} is a sparse tensor of size 3 x 3 x 3 with 4 nonzeros
(1,1,1) 1
(2,1,1) 1
(2,2,2) 1
(3,3,2) 1
An Large-Scale Example
For large-scale problems, the sumtensor class may make the difference as to whether or not a tensor can be stored in memory. Consider the following example, where 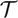 is of size
is of size 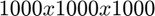 , formed from the sum of a ktensor and an sptensor.
, formed from the sum of a ktensor and an sptensor.
rng('default'); %<- Setting random seed for reproducibility of this script X1 = rand(500, 3); %Generating some factor matrices X2 = rand(500, 3); X3 = rand(500, 3); K = ktensor([1; 1; 1], X1, X2, X3); S = sptenrand([500, 500, 500], 1e-100); ST = sumtensor(K,S); %<-- Declare the sumtensor TT = full(ST); %<-- Form the sum of the tensors explicitly whos ST TT %<--Output the storage information for these variables
Name Size Bytes Class Attributes ST 500x500x500 37608 sumtensor TT 500x500x500 1000000360 tensor
The difference in memory between the full and sumtensor is a factor of 10^5! Hence we prefer to use the sumtensor object whenever possible.
Further examples of the sumtensor constructer
The sumtensor constructor can declare an empty sumtensor object, having no parts, as follows
P = sumtensor()
P is an empty sumtensor
sumtensor also supports use as a copy constructor.
S = sumtensor(P)
S is an empty sumtensor
Use ndims and size for the dimensions of a sumtensor
For a given sumtensor, ndims returns the number of modes of a sumtensor. Similarly, size returns a size array of the sumtensor.
ndims(T) size(T)
ans =
3
ans =
3 3 3
Use full to convert a sumtensor to a "generic" tensor
The full function can be used to convert a sumtensor to a generic tensor. Note that for large-scale tensors, this can a large amount of memory because each part of the sumtensor will be expanded and then summed.
full(T)
ans is a tensor of size 3 x 3 x 3 ans(:,:,1) = 2 1 1 2 1 1 1 1 1 ans(:,:,2) = 1 1 1 1 2 1 1 1 2 ans(:,:,3) = 1 1 1 1 1 1 1 1 1
Use double to convert a sumtensor to a multidimensional array
The double function can be used to convert a sumtensor to a multidimensional array. Similarly to the full expansion, this can use a prohibitive amount of memory for large-scale problems.
double(T)
ans(:,:,1) =
2 1 1
2 1 1
1 1 1
ans(:,:,2) =
1 1 1
1 2 1
1 1 2
ans(:,:,3) =
1 1 1
1 1 1
1 1 1
Matricized Khatri-Rao product of a sumtensor
The mttkrp function computes the Khatri-Rao product of a matricized tensor and a sumtensor. The required arguments are: a sumtensor X, a cell array of matrices U={U1,...,Um}, and a mode n. The cell array must consist of m matrices, where m is the number of modes in X. The number of columns of these matrices should be constant, and number of rows of matrix Ui should match the dimension of the tensor X in mode i. The matricized Khatri-Rao product operation on sumtensor distributes the operation to the summands of the sumtensor. For details of this specific computation, see the mttkrp documentation for a generic tensor. An example of the use of mttkrp follows.
U={eye(3), ones(3,3), randn(3,3)}; %<--The cell array of matrices
mttkrp(T,U,2)
ans = -0.4047 2.3659 0.3224 -0.5803 2.8714 0.3224 -0.5803 1.6632 -0.4026
Use innerprod to compute the inner product of a sumtensor
The innerprod function computes the inner product of a sumtensor T and any type of tensor. The operation is performed by distributing across each of the sumtensor's parts.
S = sptensor([1 1 1; 2 1 3; 3 2 2; 2 1 1], 1, [3,3,3]); innerprod(T,S)
ans =
6
Use norm for compatibility with the other types of tensors.
The norm function returns 0 and a warning when called on a sumtensor. The procedure of computing the Frobenius norm of a sumtensor does not distribute across its parts, and hence is not supported for sumtensors. This default behavior is provided in order to ensure compatibility of the sumtensor class with existing decomposition routines.
norm(T)
Warning: The NORM function is not supported by SUMTENSOR.
Returning zero.
ans =
0
In order avoid this default behavior and return the Frobenius norm of a sumtensor, it can be converted to a tensor using full.
norm(full(T))
ans =
6.2450
Use CP-ALS to find a CP decomposition of a sumtensor
One of the primary motivations for defining the sumtensor class is for efficient decomposition. In particular, when trying to find a CP decomposition of a tensor using alternating least squares, the subproblems can be efficiently created and solved using mttkrp and innerprod. Both of these operations can be performed more efficiently by exploiting extra structure in the tensors which form the sum, so the performance of cp_als is also improved. Consider the following example, where a cp_als is run on a sumtensor.
cp_als(T, 2)
Warning: The NORM function is not supported by SUMTENSOR.
Returning zero.
CP_ALS:
Iter 1: f = -3.738671e+01 f-delta = 3.7e+01
Iter 2: f = -3.781295e+01 f-delta = 4.3e-01
Iter 3: f = -3.781994e+01 f-delta = 7.0e-03
Iter 4: f = -3.782243e+01 f-delta = 2.5e-03
Iter 5: f = -3.782370e+01 f-delta = 1.3e-03
Iter 6: f = -3.782452e+01 f-delta = 8.2e-04
Iter 7: f = -3.782514e+01 f-delta = 6.2e-04
Iter 8: f = -3.782565e+01 f-delta = 5.1e-04
Iter 9: f = -3.782609e+01 f-delta = 4.4e-04
Iter 10: f = -3.782647e+01 f-delta = 3.8e-04
Iter 11: f = -3.782680e+01 f-delta = 3.3e-04
Iter 12: f = -3.782709e+01 f-delta = 2.9e-04
Iter 13: f = -3.782734e+01 f-delta = 2.5e-04
Iter 14: f = -3.782757e+01 f-delta = 2.2e-04
Iter 15: f = -3.782776e+01 f-delta = 2.0e-04
Iter 16: f = -3.782794e+01 f-delta = 1.7e-04
Iter 17: f = -3.782809e+01 f-delta = 1.5e-04
Iter 18: f = -3.782823e+01 f-delta = 1.4e-04
Iter 19: f = -3.782834e+01 f-delta = 1.2e-04
Iter 20: f = -3.782845e+01 f-delta = 1.1e-04
Iter 21: f = -3.782855e+01 f-delta = 9.4e-05
Final f = -3.782855e+01
ans is a ktensor of size 3 x 3 x 3
ans.lambda =
4.8661 2.3774
ans.U{1} =
0.4802 0.7336
0.5928 0.6461
0.6466 0.2109
ans.U{2} =
0.4293 0.9629
0.6286 0.2110
0.6485 0.1680
ans.U{3} =
0.4323 0.9515
0.7346 0.1117
0.5230 0.2866
It follows that in cases where 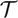 is too large for its full expansion to be stored in memory, we may still be able find a CP decomposition by exploiting the sumtensor structure.
is too large for its full expansion to be stored in memory, we may still be able find a CP decomposition by exploiting the sumtensor structure.
Note that the fit returned by cp_als is not correct for sumtensors, because the norm operation is not supported.
Basic operations (plus) for sumtensors
Sumtensors can be added to any other type of tensor. The result is a new sumtensor with the tensor appended to the parts of the original sumtensor. Note that the tensor is always appended, despite the order of the operation.
T+S %<--S is appended to the parts of T S+T %<--S is still the last part of T, despite order
ans is a sumtensor of size 3 x 3 x 3 with 3 parts
ans.part{1} is a tensor of size 3 x 3 x 3
ans.part{1}(:,:,1) =
1 1 1
1 1 1
1 1 1
ans.part{1}(:,:,2) =
1 1 1
1 1 1
1 1 1
ans.part{1}(:,:,3) =
1 1 1
1 1 1
1 1 1
ans.part{2} is a sparse tensor of size 3 x 3 x 3 with 4 nonzeros
(1,1,1) 1
(2,1,1) 1
(2,2,2) 1
(3,3,2) 1
ans.part{3} is a sparse tensor of size 3 x 3 x 3 with 4 nonzeros
(1,1,1) 1
(2,1,1) 1
(2,1,3) 1
(3,2,2) 1
ans is a sumtensor of size 3 x 3 x 3 with 3 parts
ans.part{1} is a tensor of size 3 x 3 x 3
ans.part{1}(:,:,1) =
1 1 1
1 1 1
1 1 1
ans.part{1}(:,:,2) =
1 1 1
1 1 1
1 1 1
ans.part{1}(:,:,3) =
1 1 1
1 1 1
1 1 1
ans.part{2} is a sparse tensor of size 3 x 3 x 3 with 4 nonzeros
(1,1,1) 1
(2,1,1) 1
(2,2,2) 1
(3,3,2) 1
ans.part{3} is a sparse tensor of size 3 x 3 x 3 with 4 nonzeros
(1,1,1) 1
(2,1,1) 1
(2,1,3) 1
(3,2,2) 1
Subscripted reference for sumtensors
Subscripted reference can be used to return the individual parts of a sumtensor.
T.part{1}
T.part{2}
ans is a tensor of size 3 x 3 x 3 ans(:,:,1) = 1 1 1 1 1 1 1 1 1 ans(:,:,2) = 1 1 1 1 1 1 1 1 1 ans(:,:,3) = 1 1 1 1 1 1 1 1 1 ans is a sparse tensor of size 3 x 3 x 3 with 4 nonzeros (1,1,1) 1 (2,1,1) 1 (2,2,2) 1 (3,3,2) 1
