Identities and Relationships of Tensors
There are many mathematical relationships, identities, and connections among tensors. These identities are presented here and show the versatility of the Tensor Toolbox. The propositions indicated below are references to the following report:
T.G. Kolda, Multilinear Operators for Higher-order Decompositions, Tech. Rep. SAND2006-2081, Sandia National Laboratories, 2006
Contents
rng('default'); %<- Setting random seed for reproducibility of this script
N-mode product properties
Create some data.
Y = tenrand([4 3 2]); A = rand(3,4); B = rand(3,3);
Prop 3.4(a): The order of the multiplication in different modes is irrelevant.
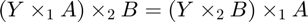
X1 = ttm( ttm(Y,A,1), B, 2); %<-- Y x_1 A x_2 B X2 = ttm( ttm(Y,B,2), A, 1); %<-- Y x_2 B x_1 A norm(X1 - X2) %<-- difference is zero
ans = 9.4206e-16
N-mode product and matricization
Generate some data to work with.
Y = tenrand([5 4 3]);
A = rand(4,5); B = rand(3,4); C = rand(2,3); U = {A,B,C};
Prop. 3.7a: N-mode multiplication can be expressed in terms of matricized tensors.
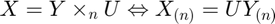
for n = 1:ndims(Y) X = ttm(Y,U,n); %<-- X = Y x_n U{n} Xn = U{n} * tenmat(Y,n); %<-- Xn = U{n} * Yn norm(tenmat(X,n) - Xn) % <-- should be zero end
ans =
0
ans =
0
ans =
0
Prop. 3.7b: We can do matricizations in various ways and still be equivalent.
X = ttm(Y,U); %<-- X = Y x_1 A x_2 B x_3 C Xm1 = kron(B,A)*tenmat(Y,[1 2])*C'; %<-- Kronecker product version Xm2 = tenmat(X,[1 2]); %<-- Matriczed version norm(Xm1 - Xm2) % <-- should be zero Xm1 = B * tenmat(Y,2,[3 1]) * kron(A,C)'; %<-- Kronecker product version Xm2 = tenmat(X,2,[3 1]); %<-- Matricized version norm(Xm1 - Xm2) % <-- should be zero Xm1 = tenmat(Y,[],[1 2 3]) * kron(kron(C,B),A)'; %<-- Vectorized via Kronecker Xm2 = tenmat(X,[],[1 2 3]); %<-- Vectorized via matricize norm(Xm1 - Xm2)
ans = 1.9230e-15 ans = 2.3630e-15 ans = 2.4146e-15
Norm of difference between two tensors
Prop. 3.9: For tensors X and Y, we have:
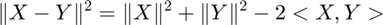
X = tenrand([5 4 3]); Y = tenrand([5 4 3]);
% The following 2 results should be equal
norm(X-Y)
sqrt(norm(X)^2 - 2*innerprod(X,Y) + norm(Y)^2)
ans =
3.1155
ans =
3.1155
This relationship makes it more convenient to compare the norm of the difference between two different tensor objects. Imagine if we have a sptensor and a ktensor and we want the norm of the difference, which may be needed to check for convergence, for example, but which is very expensive to convert to a full (dense) tensor. Because innerprod and norm are defined for all types of tensor objects, this is a handy formula.
X = sptensor(X);
Y = ktensor({[1:5]',[1:4]',[1:3]'});
% The following 2 results should be equal
norm(full(X)-full(Y))
sqrt(norm(X)^2 - 2*innerprod(X,Y) + norm(Y)^2)
ans = 148.8817 ans = 148.8817
Tucker tensor properties
The properties of the Tucker operator follow directly from the properties of n-mode multiplication.
% Initialize data
Y = tensor(1:24,[4 3 2]);
A1 = reshape(1:20,[5 4]);
A2 = reshape(1:12,[4 3]);
A3 = reshape(1:6,[3 2]);
A = {A1,A2,A3};
B1 = reshape(1:20,[4 5]);
B2 = reshape(1:12,[3 4]);
B3 = reshape(1:6,[2 3]);
B = {B1,B2,B3};
Proposition 4.2a
X = ttensor(ttensor(Y,A),B)
X is a ttensor of size 4 x 3 x 2
X.core is a ttensor of size 5 x 4 x 3
X.core.core is a tensor of size 4 x 3 x 2
X.core.core(:,:,1) =
1 5 9
2 6 10
3 7 11
4 8 12
X.core.core(:,:,2) =
13 17 21
14 18 22
15 19 23
16 20 24
X.core.U{1} =
1 6 11 16
2 7 12 17
3 8 13 18
4 9 14 19
5 10 15 20
X.core.U{2} =
1 5 9
2 6 10
3 7 11
4 8 12
X.core.U{3} =
1 4
2 5
3 6
X.U{1} =
1 5 9 13 17
2 6 10 14 18
3 7 11 15 19
4 8 12 16 20
X.U{2} =
1 4 7 10
2 5 8 11
3 6 9 12
X.U{3} =
1 3 5
2 4 6
AB = {B1*A1, B2*A2, B3*A3};
Y = ttensor(Y,AB)
Y is a ttensor of size 4 x 3 x 2
Y.core is a tensor of size 4 x 3 x 2
Y.core(:,:,1) =
1 5 9
2 6 10
3 7 11
4 8 12
Y.core(:,:,2) =
13 17 21
14 18 22
15 19 23
16 20 24
Y.U{1} =
175 400 625 850
190 440 690 940
205 480 755 1030
220 520 820 1120
Y.U{2} =
70 158 246
80 184 288
90 210 330
Y.U{3} =
22 49
28 64
norm(full(X)-full(Y)) %<-- should be zero
ans =
0
Proposition 4.2b
Y = tensor(1:24,[4 3 2]);
X = ttensor(Y,A);
Apinv = {pinv(A1),pinv(A2),pinv(A3)};
Y2 = ttensor(full(X),Apinv);
norm(full(Y)-full(Y2)) %<-- should be zero
ans = 1.0259e-12
Proposition 4.2c
Y = tensor(1:24,[4 3 2]);
rand('state',0);
Q1 = orth(rand(5,4));
Q2 = orth(rand(4,3));
Q3 = orth(rand(3,2));
Q = {Q1,Q2,Q3};
X = ttensor(Y,Q)
X is a ttensor of size 5 x 4 x 3
X.core is a tensor of size 4 x 3 x 2
X.core(:,:,1) =
1 5 9
2 6 10
3 7 11
4 8 12
X.core(:,:,2) =
13 17 21
14 18 22
15 19 23
16 20 24
X.U{1} =
-0.4727 0.5608 0.0275 -0.3954
-0.4394 -0.4243 0.3178 0.5707
-0.4659 -0.6116 -0.1037 -0.5982
-0.4209 0.3259 0.5458 0.1138
-0.4350 0.1587 -0.7679 0.3837
X.U{2} =
-0.2570 0.1257 0.8908
-0.3751 -0.2111 0.2636
-0.4640 -0.7988 -0.1591
-0.7602 0.5492 -0.3341
X.U{3} =
-0.3907 -0.0625
-0.8045 -0.4616
-0.4473 0.8849
Qt = {Q1',Q2',Q3'};
Y2 = ttensor(full(X),Qt)
norm(full(Y)-full(Y2)) %<-- should be zero
Y2 is a ttensor of size 4 x 3 x 2
Y2.core is a tensor of size 5 x 4 x 3
Y2.core(:,:,1) =
1.4195 -0.0317 -1.4127 -0.3848
-0.7708 0.2767 1.3323 0.4969
8.6788 -0.0536 -8.3316 -2.1970
-3.0735 0.1529 3.2424 0.9267
2.9652 0.0889 -2.6130 -0.6316
Y2.core(:,:,2) =
4.6979 -0.3995 -5.3170 -1.6004
-2.2186 0.8006 3.8440 1.4349
28.9023 -2.1266 -31.9901 -9.4788
-10.0638 1.0545 11.8230 3.6490
10.0122 -0.4854 -10.5344 -3.0047
Y2.core(:,:,3) =
-3.4733 0.9238 5.3001 1.8807
0.9310 -0.3464 -1.6360 -0.6138
-21.7522 5.7319 33.0762 11.7190
7.2102 -1.9498 -11.0723 -3.9398
-7.8266 2.0225 11.8142 4.1724
Y2.U{1} =
-0.4727 -0.4394 -0.4659 -0.4209 -0.4350
0.5608 -0.4243 -0.6116 0.3259 0.1587
0.0275 0.3178 -0.1037 0.5458 -0.7679
-0.3954 0.5707 -0.5982 0.1138 0.3837
Y2.U{2} =
-0.2570 -0.3751 -0.4640 -0.7602
0.1257 -0.2111 -0.7988 0.5492
0.8908 0.2636 -0.1591 -0.3341
Y2.U{3} =
-0.3907 -0.8045 -0.4473
-0.0625 -0.4616 0.8849
ans =
9.8758e-14
Tucker operator and matricized tensors
The Tucker operator also has various epressions in terms of matricized tensors and the Kronecker product. Proposition 4.3a
Y = tensor(1:24,[4 3 2]);
A1 = reshape(1:20,[5 4]);
A2 = reshape(1:12,[4 3]);
A3 = reshape(1:6,[3 2]);
A = {A1,A2,A3};
X = ttensor(Y,A)
for n = 1:ndims(Y)
rdims = n;
cdims = setdiff(1:ndims(Y),rdims);
Xn = A{n} * tenmat(Y,rdims,cdims) * kron(A{cdims(2)}, A{cdims(1)})';
norm(tenmat(full(X),rdims,cdims) - Xn) % <-- should be zero
end
X is a ttensor of size 5 x 4 x 3
X.core is a tensor of size 4 x 3 x 2
X.core(:,:,1) =
1 5 9
2 6 10
3 7 11
4 8 12
X.core(:,:,2) =
13 17 21
14 18 22
15 19 23
16 20 24
X.U{1} =
1 6 11 16
2 7 12 17
3 8 13 18
4 9 14 19
5 10 15 20
X.U{2} =
1 5 9
2 6 10
3 7 11
4 8 12
X.U{3} =
1 4
2 5
3 6
ans =
0
ans =
0
ans =
0
Orthogonalization of Tucker factors
Proposition 4.4
Y = tensor(1:24,[4 3 2]);
A1 = rand(5,4);
A2 = rand(4,3);
A3 = rand(3,2);
A = {A1,A2,A3};
X = ttensor(Y,A)
X is a ttensor of size 5 x 4 x 3
X.core is a tensor of size 4 x 3 x 2
X.core(:,:,1) =
1 5 9
2 6 10
3 7 11
4 8 12
X.core(:,:,2) =
13 17 21
14 18 22
15 19 23
16 20 24
X.U{1} =
0.2026 0.3795 0.3046 0.5417
0.6721 0.8318 0.1897 0.1509
0.8381 0.5028 0.1934 0.6979
0.0196 0.7095 0.6822 0.3784
0.6813 0.4289 0.3028 0.8600
X.U{2} =
0.8537 0.8216 0.3420
0.5936 0.6449 0.2897
0.4966 0.8180 0.3412
0.8998 0.6602 0.5341
X.U{3} =
0.7271 0.5681
0.3093 0.3704
0.8385 0.7027
[Q1,R1] = qr(A1);
[Q2,R2] = qr(A2);
[Q3,R3] = qr(A3);
R = {R1,R2,R3};
Z = ttensor(Y,R);
norm(X) - norm(Z) %<-- should be zero
ans = -5.6843e-14
Kruskal operator properties
Proposition 5.2
A1 = reshape(1:10,[5 2]);
A2 = reshape(1:8,[4 2]);
A3 = reshape(1:6,[3 2]);
K = ktensor({A1,A2,A3});
B1 = reshape(1:20,[4 5]);
B2 = reshape(1:12,[3 4]);
B3 = reshape(1:6,[2 3]);
X = ttensor(K,{B1,B2,B3})
Y = ktensor({B1*A1, B2*A2, B3*A3});
norm(full(X) - full(Y)) %<-- should be zero
X is a ttensor of size 4 x 3 x 2
X.core is a ktensor of size 5 x 4 x 3
X.core.lambda =
1 1
X.core.U{1} =
1 6
2 7
3 8
4 9
5 10
X.core.U{2} =
1 5
2 6
3 7
4 8
X.core.U{3} =
1 4
2 5
3 6
X.U{1} =
1 5 9 13 17
2 6 10 14 18
3 7 11 15 19
4 8 12 16 20
X.U{2} =
1 4 7 10
2 5 8 11
3 6 9 12
X.U{3} =
1 3 5
2 4 6
ans =
0
Proposition 5.3a (second part)
A1 = reshape(1:10,[5 2]);
A2 = reshape(1:8,[4 2]);
A3 = reshape(1:6,[3 2]);
A = {A1,A2,A3};
X = ktensor(A);
rdims = 1:ndims(X);
Z = double(tenmat(full(X), rdims, []));
Xn = khatrirao(A{rdims},'r') * ones(length(X.lambda),1);
norm(Z - Xn) % <-- should be zero
ans =
0
cdims = 1:ndims(X);
Z = double(tenmat(full(X), [], cdims));
Xn = ones(length(X.lambda),1)' * khatrirao(A{cdims},'r')';
norm(Z - Xn) % <-- should be zero
ans =
0
Proposition 5.3b
A1 = reshape(1:10,[5 2]);
A2 = reshape(1:8,[4 2]);
A3 = reshape(1:6,[3 2]);
A = {A1,A2,A3};
X = ktensor(A);
for n = 1:ndims(X)
rdims = n;
cdims = setdiff(1:ndims(X),rdims);
Xn = khatrirao(A{rdims}) * khatrirao(A{cdims},'r')';
Z = double(tenmat(full(X),rdims,cdims));
norm(Z - Xn) % <-- should be zero
end
ans =
0
ans =
0
ans =
0
Proposition 5.3a (first part)
X = ktensor(A); for n = 1:ndims(X) cdims = n; rdims = setdiff(1:ndims(X),cdims); Xn = khatrirao(A{rdims},'r') * khatrirao(A{cdims})'; Z = double(tenmat(full(X),rdims,cdims)); norm(Z - Xn) % <-- should be zero end
ans =
0
ans =
0
ans =
0
Norm of Kruskal operator
The norm of a ktensor has a special form because it can be reduced to summing the entries of the Hadamard product of N matrices of size R x R. Proposition 5.4
A1 = reshape(1:10,[5 2]);
A2 = reshape(1:8,[4 2]);
A3 = reshape(1:6,[3 2]);
A = {A1,A2,A3};
X = ktensor(A);
M = ones(size(A{1},2), size(A{1},2));
for i = 1:numel(A)
M = M .* (A{i}'*A{i});
end
norm(X) - sqrt(sum(M(:))) %<-- should be zero
ans =
0
Inner product of Kruskal operator with a tensor
The inner product of a ktensor with a tensor yields Proposition 5.5
X = tensor(1:60,[5 4 3]);
A1 = reshape(1:10,[5 2]);
A2 = reshape(2:9,[4 2]);
A3 = reshape(3:8,[3 2]);
A = {A1,A2,A3};
K = ktensor(A);
v = khatrirao(A,'r') * ones(size(A{1},2),1);
% The following 2 results should be equal
double(tenmat(X,1:ndims(X),[]))' * v
innerprod(X,K)
ans =
935340
ans =
935340
